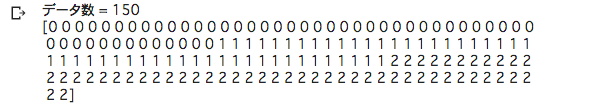k近傍法
K近傍法(K Nearest Neighbors)は、さっくり言うと、「回帰や分類を行う際に、似たようなデータをk個集めてそれらの多数決から目的とする値を求める」という手法です。
- 回帰問題
検証データと似たk個のデータのそれぞれの値の平均値や中央値、もしくは重み付けした集計値を予測結果に用います。
- クラス分類
検証データと似たk個のデータそれぞれの「クラス」でもっとも数が多いクラスにデータを分類します。(多数決の原理です)
KNN実装方法
① 学習データ(ラベル付け)とテストデータを用意する
② Kの値を決める
③ 全てのテストデータに対して、下記の処理を行う。
③-1 学習データとの距離を算出する。距離の算出には、一般的にユークリッド距離が使われる。
③-2 算出した距離をリストに保存して、ソートする。
③-3 距離は一番近いK個学習データを選べる。
③-4 数が多いクラスにデータを分類する。
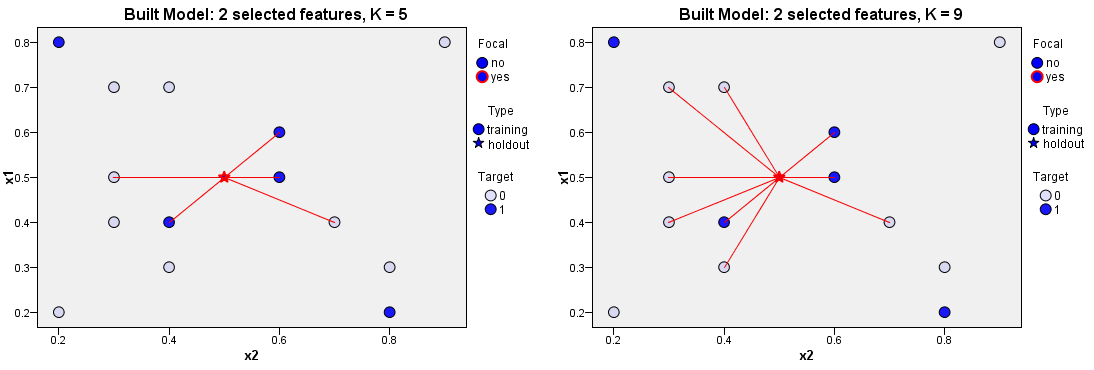
K値の特徴
K の値によって精度が変わるため、最適な K の値を設定する必要があります。
| K | 特徴 |
|---|---|
| 小さい値 | ノイズに弱い |
| 大きい値 | 精度が下がる |
クラス分類
クラス分類には、KNeighborsClassifier クラスを使用します。
実際に分類を行ってみます。
アヤメという花の分類を行います。
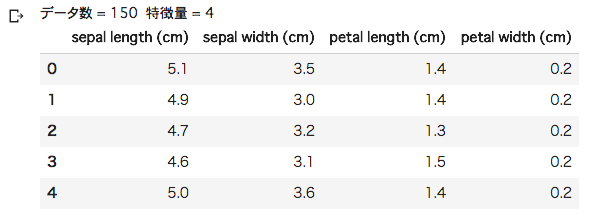
特徴量として、萼(がく)片の長さ・幅、花びらの長さ・幅の4種類があり、
分類クラスとして、Setosa、Versicolor、Virgínia の3種類があります。
%matplotlib inline import numpy as np import pandas as pd import matplotlib.pyplot as plt from sklearn.model_selection import train_test_split # アヤメデータセット読み込み from sklearn.datasets import load_iris iris = load_iris() # 特徴量 X = iris.data # 目的変数 Y = iris.target
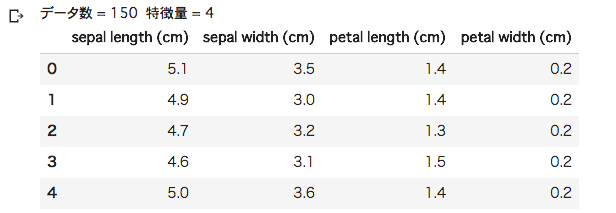
# データ表示(特徴量) print("データ数 = %d 特徴量 = %d" % (X.shape[0], X.shape[1])) pd.DataFrame(X, columns=iris.feature_names).head()
# データ表示(目的変数) print("データ数 = %d" % (Y.shape[0])) print(Y)
# トレーニング・テストデータ分割 X_train, X_test, Y_train, Y_test = train_test_split(X, Y, random_state=0) # # K-近傍法 # from sklearn.neighbors import KNeighborsClassifier list_nn = [] list_score = [] for k in range(1, 31): # K = 1~30 # KNeighborsClassifier knc = KNeighborsClassifier(n_neighbors=k) knc.fit(X_train, Y_train) # 予測 Y_pred = knc.predict(X_test) # 評価 R^2 score = knc.score(X_test, Y_test) print("[%d] score: {:.2f}".format(score) % k) list_nn.append(k) list_score.append(score) # プロット plt.ylim(0.9, 1.0) plt.xlabel("n_neighbors") plt.ylabel("score") plt.plot(list_nn, list_score)
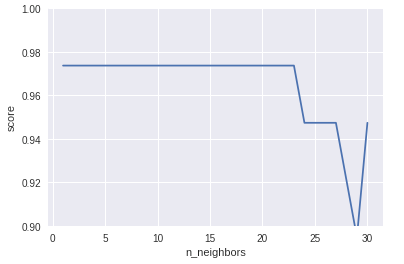
K = 1~30 まで実行しました。
K = 1~23 までの精度は 97% ですが、K = 24 以降は精度が下がっています。
K の値は、少ない数値で問題なさそうです。
回帰分析
回帰分析には、KNeighborsRegressor クラスを使用します。
ボストン住宅価格データの回帰分類を行います。
特徴量として 犯罪発生率や住宅区画の密集度など 13種類があり、
目的変数として、住宅価格があります。
今回は、特徴量として部屋数を使い住宅価格を予測します。
# ボストン住宅価格データセット from sklearn import datasets boston = datasets.load_boston() # 説明変数 X = boston.data # 目的変数 Y = boston.target
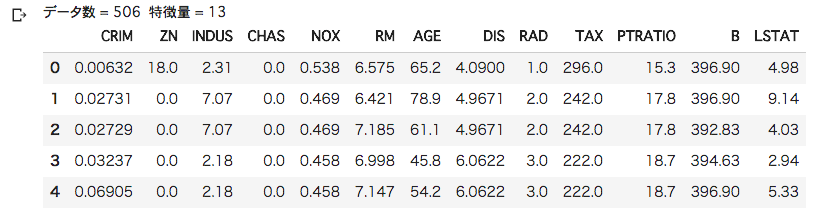
# データ表示(特徴量) print("データ数 = %d 特徴量 = %d" % (X.shape[0], X.shape[1])) pd.DataFrame(X, columns=boston.feature_names).head()
# データ表示(目的変数) print("データ数 = %d" % (Y.shape[0])) print(Y[:10]) # 先頭 10件表示

# 説明変数に部屋数のみ使用 X = boston.data[:, [5]] # 部屋数 # トレーニング・テストデータ分割 X_train, X_test, Y_train, Y_test = train_test_split(X, Y, random_state=0) # プロット plt.xlabel("RM") plt.ylabel("Target") plt.plot(X_train, Y_train, "o")
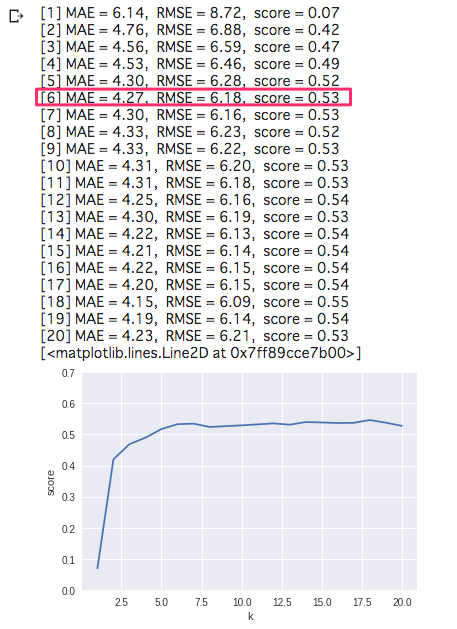
from sklearn.neighbors import KNeighborsRegressor from sklearn.metrics import mean_squared_error from sklearn.metrics import mean_absolute_error list_k = [] list_score = [] for k in range(1, 21): # KNeighborsClassifier knr = KNeighborsRegressor(n_neighbors=k) knr.fit(X_train, Y_train) # 予測 Y_pred = knr.predict(X_test) # # 評価 # # 平均絶対誤差(MAE) mae = mean_absolute_error(Y_test, Y_pred) # 平方根平均二乗誤差(RMSE) rmse = np.sqrt(mean_squared_error(Y_test, Y_pred)) # スコア R^2 score = knr.score(X_test, Y_test) print("[%d] MAE = %.2f, RMSE = %.2f, score = %.2f" % (k, mae, rmse, score)) list_k.append(k) list_score.append(score) # プロット plt.ylim(0, 0.7) plt.xlabel("k") plt.ylabel("score") plt.plot(list_k, list_score)
K = 6 以降、ほとんど変化がありません。
K 値は 6 で良いようです。
参考リンク:https://qiita.com/fujin/items/128ed7188f7e7df74f2c